BILANGAN BULAT

Table of Contents

Bilangan bulat dibedakan menjadi tiga bagian, yaitu bilangan bulat negatif, nol, dan bilangan bulat positif. Pada garis bilangan, bilangan bulat positif terletak di kanan bilangan nol. Sedangkan bilangan bulat negatif terletak di kiri nol. Untuk lebih jelasnya, perhatikan garis bilangan berikut.

Istilah lain dari bilangan bulat positif adalah bilangan asli. Sedangkan, gabungan dari bilangan bulat positif dan nol disebut bilangan cacah.

Membandingkan Bilangan Bulat

Untuk membandingkan dua bilangan bulat yang mendekati nol (angka penyusun bilangan tersebut sedikit), kalian cukup melihat posisi kedua bilangan tersebut pada garis bilangan. Tentunya hal itu tidak sulit. Bilangan yang lebih besar selalu berada di kanan bilangan yang lebih kecil. Namun untuk membandingkan bilangan-bilangan bulat positif yang sangat besar, atau bilangan-bilangan bulat negatif yang sangat kecil, tentunya tidak efektif menggunakan garis bilangan.

Untuk membandingkan bilangan bulat positif yang sangat besar atau bilangan bulat negatif yang sangat kecil, kalian bisa dengan mengamati angka-angka penyusunnya. Bilangan tersusun atas angka 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9.

Bilangan 7 "baca tujuh" tersusun dari angka 7 saja.

Bilangan 12 "baca dua belas" tersusun dari angka 1 dan 2.

Bilangan 123 "baca seratus dua puluh tiga" tersusun dari angka 1, 2, dan 3.

Bilangan 6123987 "baca enam juta seratus dua puluh tiga ribu sembilan ratus delapan puluh tujuh" tersusun dari angka 1, 2, 3, 6, 7, 8, dan 9.

Angka 6 pada posisi jutaan, bernilai 6 × 1.000.000 = 6.000.000.

Angka 1 pada posisi ratusribuan, bernilai 1 × 100.000 = 100.000.

Angka 2 pada posisi puluhribuan, bernilai 2 × 10.000 = 20.000.

Angka 3 pada posisi ribuan, bernilai 3 × 1.000 = 3.000.

Angka 9 pada posisi ratusan, bernilai 9 × 100 = 900.

Angka 8 pada posisi puluhan, bernilai 8 × 10 = 80.

Angka 7 pada posisi satuan, bernilai 7 × 1 = 1.

Tabel 1.1 Nilai angka pada bilangan

Nilai Angka	Baca
1	Satu
10	Sepuluh
100	Seratus
1.000	Seribu
10.000	Sepuluh ribu
100.000	Seratus ribu
1.000.000	Satu juta
10.000.000	Sepuluh juta
100.000.000	Seratus juta
1.000.000.000	Satu milyar
10.000.000.000	Sepuluh milyar
100.000.000.000	Seratus milyar
1.000.000.000.000	Satu triliun

CONTOH 1

Tentukan manakah yang lebih besar (kuantitas) antara 47653 dengan 8699.

ALTERNATIF PENYELESAIAN

Kedua bilangan tersebut memiliki banyak angka penyusun yang berbeda. Bilangan 47653 memiliki lima angka penyusun. Sedangkan 8699 hanya memiliki empat angka penyusun. Oleh karena itu, untuk membandingkan kedua bilangan tersebut kita dapat menentukan dengan mudah, yaitu 47654 lebih besar dari 8699 karena angka penyusunnya lebih banyak.

Angka 4 pada bilangan 47653 menempati nilai puluh ribuan, sehingga nilainya adalah 40.000 (dibaca: empat puluh ribu). Nilai angka terbesar pada bilangan 8699 adalah ribuan yang ditempati oleh angka “8“, sehingga nilainya adalah 8.000 (dibaca: depalan ribu). Tanpa melihat nilai angka lain pada kedua bilangan tersebut kita bisa menentukan bahwa 47654 lebih besar dari 8699.

Jadi, 47654 lebih besar dari 8699.

---

CONTOH 2

Tentukan manakah yang lebih besar (kuantitas) antara 8592 dengan 8631

ALTERNATIF PENYELESAIAN

Kedua bilangan sama-sama tersusun oleh empat angka. Nilai angka 6 (bernilai 600) pada bilangan 8631 lebih besar dari nilai angka 5 (bernilai 500) pada bilangan 8592. Oleh karena itu, 8631 lebih dari 8592.

Kedua bilangan tersebut mempunyai banyak angka penyusun yang sama, yaitu empat. Nilai angka terbesar (yaitu ribuan) sama-sama ditempati oleh angka “8” sehingga nilainya sama, yaitu 8.000. Nilai angka terbesar kedua (yaitu ratusan) pada bilangan 8592 ditempati oleh angka “5”, sehingga nilainya 500. Sedangkan pada bilangan 8631 ditempati oleh angka “6”, sehingga nilainya adalah 600. Dengan membandingan kedua bilangan tersebut (500 dan 600) kita dapat menentukan bahwa 600 lebih besar dari 500.

Jadi, 8631 lebih besar dari 8592.

---

Operasi Penjumlahan dan Pengurangan Bilangan Bulat

CONTOH 3

Mia mempunyai 3 boneka di rumahnya. Ketika ulang tahun, Mia mendapatkan hadiah sebanyak 4 boneka lagi. Berapakah boneka yang dimiliki Mia sekarang?

ALTERNATIF PENYELESAIAN

Kita bisa menggunakan garis bilangan di bawah ini untuk memaknai penjumlahan 3 ditambah 4. Karena Mia memilik 3 boneka, maka dari titik asal (0) bergerak 3 satuan ke kanan. Kemudian, karena mendapatkan 4 boneka lagi, berarti terus bergerak 4 satuan ke kanan. Sehingga hasil akhirnya adalah 7.

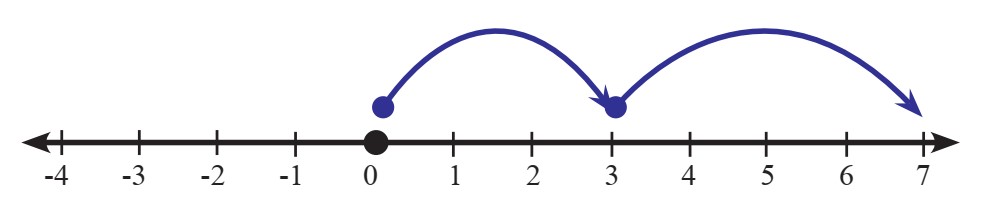
Jadi, boneka yang dimiliki Mia sekarang adalah 7 boneka.

---

Selisih antara dua bilangan bulat sama dengan jarak kedua bilangan tersebut pada garis bilangan. Misalnya,

1. selisih antara 1 dengan 4 adalah 3 satuan,
2. selisih antara -2 dengan 3 adalah 5 satuan.

Perhatikan ilustrasi berikut!

CONTOH 4

Nia mempunyai 6 pasang sepatu di rumahnya. Karena sedang senang hati, Nia memberikan 2 pasang sepatunya kepada sepupunya. Berapakah pasang sepatu yang dimiliki Nia sekarang?

ALTERNATIF PENYELESAIAN

Bentuk dari soal tersebut adalah 6 − 2 = ...

Awalnya Nia memiliki 6 pasang sepatu, maka bergerak dari titik nol ke kanan 6 satuan. Karena dikurang 2 pasang sepatu, berarti panah berbalik arah ke kiri 2 satuan. Sehingga hasil akhirnya adalah 4.

Perhatikan bahwa 6 − 2 sama dengan penjumlahan 6 + (−2). Panah ke kiri menunjukkan arah pengurangan oleh bilangan positif atau penjumlahan dengan bilangan negatif (−).

Jadi, banyak sepatu yang dimiliki Nia sekarang adalah 6 − 2 = 4 pasang.

---

Sifat-Sifat Operasi Penjumlahan dan Pengurangan pada Bilangan Bulat

Sifat 1: Komutatif

Secara umum, Jika a dan b adalah sebarang bilangan bulat, maka berlakua+b=b+a

Sifat 2: Asosiatif

Secara umum, jika a, b, dan c adalah sebarang bilangan bulat, maka berlaku a + (b+c) = (a+b) + c

Sifat Tertutup: Bilangan bulat ditambah atau dikurang bilangan bulat menghasilkan bilangan bulat.

Jika a, b bilangan bulat dan a + b = c, maka c merupakan bilangan bulat.

Bilangan genap ditambah bilangan genap menghasilkan bilangan genap

Contoh, 2 + 4 = 6.

Bilangan genap ditambah bilangan ganjil menghasilkan bilangan ganjil

Contoh, 2 + 3 = 5.

Bilangan ganjil ditambah bilangan ganjil menghasilkan bilangan genap

Contoh, 3 + 3 = 6.

Operasi Perkalian dan Pembagian Bilangan Bulat

Perkalian Bilangan Bulat

Secara umum, untuk a elemen bilangan bulat positif dan b elemen bilangan bulat, a × b diartikan menjumlahkan b sebanyak a kali.

a\times b=\underbrace{b+b+\cdots+b}_{a\text{ kali}}

Pada operasi perkalian juga berlaku sifat komutatif, asosiatif, dan distributif. Untuk sebarang bilangan bulat a, b, dan, c berlaku

Komutatif

a\times b=b\times a

Asosiatif

(a\times b)\times c=a\times(b\times c)

Distributif

Perkalian terhadap penjumlahan

a\times(b+c)=a\times b+a\times c

Perkalian terhadap pengurangan

a \times (b - c) = a \times b - a \times c

Perkalian dua bilangan bulat tak nol

Bilangan I		Bilangan II		Hasil
Positif (+)	×	Positif (+)	=	Positif (+)
Positif (+)	×	Negatif (−)	=	Negatif (−)
Negatif (−)	×	Positif (+)	=	Negatif (−)
Negatif (−)	×	Negatif (−)	=	Positif (+)

Keterangan: Positif (+) : Sebarang bilangan bulat positif
Negatif (−) : Sebarang bilangan bulat negatif

Pembagian Bilangan Bulat

Secara umum jika a, b, dan c adalah bilangan bulat.

Jika a × b = c maka a=\dfrac{c}b, dengan b ≠ 0 atau Jika a × b = c maka b=\dfrac{c}a, dengan a ≠ 0